1. Improve Recruitment Effectiveness
HR analytics lets HR make better decisions on the basis of historical information of employee performance. For example, if data suggests that some of your best talent have certain education background, hobbies or profile, you will be able to screen profiles from the candidates pool and get those who are most likely to be successful. This would mean lower cost of recruitment, reduction attrition in future and better business results. The availability of online databases, applications, profiles in social media and career directories, documents, etc. today enables how we can improve the effectiveness of recruitment and easily learn more about applicants.
Similarly, we can use online databased and career directories to build profiles and job descriptions based on how other organizations define such roles and the availability of talent pool in the market. This is higher success rate during not only recruitment but also in retention
2. Build Productive Workforce
Using historic data of employee performance and specific conditions that led an employee to performance better, HR managers can using Clustering Models to put together teams of like minded employees where every individual performs it his/her best. Similarly, inconsistent performance, spikes or drops in performance can help HR analysts identify key drivers for such pattern.
3. Reducing Attrition by Predicting it
This is one of the most widely used application or example for HR Analytics. By using historic data related to employees it is possible to used Machine Learning (ML) classification models is very accurately predict employees who are most likely to leave the organization. This is called as Predictive Model for Employee Attrition. The model provides the propensity or probability that an employee would leave in near future. This data based approach can replace RAG (Red/Amber/Green) colour codes that HRBP’s use to classify employees based on high flight risk.
4. Performance Management
Linking Performance to Pay is a ever green topic in HR. With performance data that goes beyond performance rating, C&B professionals can build statistical models to validate if the increased compensation and benefits to an individual can result in justifiable business performance improvement. Further data analytics can be used to profile employees based on the value they see various benefits provided by the organization and personalize the package.
5. L&D Effectiveness
L&D can play pivotal in enhancing business performance and building a future fit workforce by using the data to identify training needs, establish quantitative effectiveness measures for L&D interventions and statistically prove effectiveness of the program. For example, using wearables, L&D professionals can capture real time data of employees heart rate, to ascertain the effectiveness of the learning module covered in training. Data can be used to design effective intervention.
And most importantly, L&D can rescue themselves from the perception of being providers of different career development programmes that deplete a large part of the company’s budget.
#nilakantasrinivasan-j #canopus-business-management-group #B2B-client-centric-growth #HR-analytics
In the recent years, most business functions have undergone a transformation because of the power of Big Data, Cloud Storage and Analytics. The Digitization wave that is sweeping the industry now is nothing but an outcome of the synergy of various technology developments over the past 2 decades. HR is no exception to this. HR Analytics and Big Data have provided the ability to HR leaders to take “intuitions” out of their decisions, that have been the norm before and replace that with informed decisions based on data. The use of HR analytics has made official decisions more promising and accurate.
For this reason, today many companies invest tremendous resources on talent management tools and skilled staff including data scientists, analytics and analysts.
Nevertheless, there’s a lot more to do in this area. According to a Deloitte survey, 3 out of four businesses (75%) believe the data analytics use is “important” but only 8% think that their organisation, is strong in analytics. (The same figure as in 2014).
HR Analytics can touch every division of HR and improve its decision making including Talent Acquisition and Management, Compensation and Benefits, Performance Management, HR Operations, Learning and Development, Leadership Development, etc. .
Most organizations today sit on a pile of data, thanks to HRMS & Cloud storage. However, in the absence of a proper HR analytics tool or necessary capability in HR professionals, these useful data or information we are talking about might be scattered and unused. Organizations are now getting to accept that Analytics is more about capability and less about acquiring fancy technological tools.
A HR Professional with right Analytics capability can interpret and transform this valuable data in useful statistics using HR and big data analytics to insights. HR will determine what to do on the basis of the results until trends are illustrated. The impact of HR metrics on organisational performance is analysed using analytics and that can enables leaders to take proactive decisions.
HR Analytics can also help in addressing problems that organizations face. For example, High performers exit an organisation more often than low-performers, and if so, what leads to that turnover? Data based insights can empower business leaders to take right decisions regarding talent rather than mulling over intuitions or finger pointing between HR and Business.
Here are 6 big Benefits of HR Analytics
Improve HR alignment to Business Strategy
It is very common to see that HR function in isolation vis-a vis the business. If you don’t agree with me, find out what business leaders do when HR slides are put up in Management Committee presentations and what HR head does when Business slides are put up? Most HR metrics, processes, & policies are benchmarked with respect to industry and competition, but very rarely they are aligned to hard hitting reality of their own business. For example, just by aligning HR metrics to business metrics, such as HR Cost per Revenue or HR Cost per unit sold, Revenue per employee, Average Lead time to productivity, HR professionals can take the first step towards better alignment to business strategy.
Complex decisions regarding the hiring, employee performance, career progression, internal movements, etc have direct impact on business strategy. When HR Analytics can provide insights on which employee is most likely to be productive in a new role, who is most likely to accept a internal job movement based on historic data, how long is it likely to take to close a critical position, based on data, HR seamlessly aligns with Business needs and strategy.
Creating meaningful HR Processes
Not long ago, HR was marred with policy paralysis. Organizations had HR policies for everything. Processes were built for those policies and not for people who would use, manage or benefit from it. HR Automation is many ways has helped organizations their standardize processes. Whether it’s about Leave Approval, Employee Escalations, Reimbursements, Payroll, etc.
When we have meaningful data that provide us insights about processes, we will be able to take decisions that matter the most for our employees. For example, an organization introduced flexible working hours for its executives just because everyone in the market is doing that. And because few employees asked for it. Few weeks into the few flexi working system, surprisingly, they found that most employees wouldn’t avail this benefit. Data suggested that 90% of employees commute to work using company shuttle as the organization is located in an industrial suburb. So just by looking into data, organizations can build processes that are meaningful rather than what is an industry norm.
Another popular example is that of Google reducing the number of rounds of interviews based on data, thereby improving candidate experience, interviewer experience and cutting down on the lead time to hire.
Enhance Employee Experience
Insights from the data across employee lifecycle can help HR managers emotionally connect with employees, build personalization , etc., For example, if an employee struggles to comply with certain HR policies, data of can provide timely insights on how the organization can support the employee in bettering his experience during the tenure thereby creating a win-win situation.
Improve HR Effectiveness
Data insights from HR analytics can suggest to us which candidates are likely to get selected, which are likely to perform well, if selected, thereby enabling the business to increase its performance and success rate. Such insights can be used in not only hiring, but in career progression, retention, learning and development, etc., For example, it would be an invaluable insight if HR can suggest which employees are likely to perform together without conflict, if business wants a put a new team together.
Reduce HR related costs
HR Analytics can help HR managers identify blind spots as far as leakage is concerned. For example, how much increment should we give a candidate, what are the increment slabs that the organization have so as to keep employee attrition within certain level, and so on.
Build a Great Place to Work
Ultimately, it is every HR head’s dream to build an organization that employee’s love to work for -One where employees wake up every morning and say, ‘here’s another great day’. Instead of being a copy cat and experimenting with what works for other best employers in your industry or country, delving into data can cull out insights on what your employees love, relish and dislike.
#nilakantasrinivasan-j #canopus-business-management-group #B2B-client-centric-growth #HR-analytics #big-data #HR-metrics
- Results of this survey, your details or information you share, including your organization name will NOT be published anywhere
- This is NOT a prospecting pitch to solicit business opportunity
Is there a difference between Six Sigma and Lean Six Sigma?
Lean and Six Sigma are close cousins in the process improvement world and they have lot of commonalities. Now we will talk about the difference between Six Sigma and Lean Six Sigma.
Six Sigma uses a data centric analytical approach to problem solving and process improvements. That means, there would be time and effort in data collection and analysis. While this sounds very logical to any problem solving approach, there can be practical challenges.
For example, some times we may need data and analysis to be even prove the obvious. That is lame.
On the other hand, Lean Six Sigma brings in some of the principles of Lean. Lean is largely a pragmatic and prescriptive approach. Which implies that we will look at data and practically validate that problem and move on to prescriptive solutions.
Thus combining Lean with Six Sigma, helps in reducing the time and effort needed to analyze or improve a situation. Lean will bring in a set of solutions that are tried and tested for a situation. For example, if you have high inventory, that Lean would suggest you to implement Kanban.
Lean is appealing because most often it simplifies the situation and that may not be always true with Six Sigma. However the flip side to Lean is that if the system have been improved several times and reached a certain level of performance and consistency, Lean can bring out any further improvement unless we approach the problem with Six Sigma lens, using extensive data collection and analysis.
Looking at the body of knowledge of Six Sigma and Lean Six Sigma, you will find that Lean Six Sigma courses following tools:
- Cost of Poor Quality
- Lean Principles
- Definition, Origin, Principles & Goals of Lean
- Value, Value Stream, Concept of Muda(Waste) & Categories of Waste
- 7 Types of Wastes, How to Identify them, & Waste Identification Template
- Value Stream Mapping (VSM), Symbols, Benefits & Procedure
- Push System, Pull System, Single Piece Flow, 5S, Kaizen, SMED, Poka-Yoke
- Types of Poka-Yoke – Shut Down, Prevention, Warning, Instructions
- Heijunka & Visual Control
#nilakantasrinivasan-j #canopus-business-management-group #B2B-client-centric-growth #Lean-six-sigma #six-sigma-green-belt-certification #six-sigma-black-belt-certification
Pima Diabetes Data Analytics – Neil¶
Here are the set the analytics that has been run on this data set
- Data Cleaning to remove zeros
- Data Exploration for Y and Xs
- Descriptive Statistics – Numerical Summary and Graphical (Histograms) for all variables
- Screening of variables by segmenting them by Outcome
- Check for normality of dataset
- Study bivariate relationship between variables using pair plots, correlation and heat map
- Statistical screening using Logistic Regression
- Validation of the model its precision and ploting of confusion matrix
Importing necessary packages¶
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(color_codes =True)
%matplotlib inline
Importing the Diabetes CSV data file¶
- Import the data and test if all the columns are loaded
- The Data frame has been assigned a name of ‘diab’
diab=pd.read_csv("diabetes.csv")
diab.head()
About data set¶
In this data set, Outcome is the Dependent Variable and Remaining 8 variables are independent variables.
Finding if there are any null and Zero values in the data set¶
diab.isnull().values.any()
## To check if data contains null values
Inference:¶
- Data frame doesn’t have any NAN values
- As a next step, we will do preliminary screening of descriptive stats for the dataset
diab.describe()
## To run numerical descriptive stats for the data set
Inference at this point¶
- Minimum values for many variables are 0.
- As biological parameters like Glucose, BP, Skin thickness,Insulin & BMI cannot have zero values, looks like null values have been coded as zeros
- As a next step, find out how many Zero values are included in each variable
(diab.Pregnancies == 0).sum(),(diab.Glucose==0).sum(),(diab.BloodPressure==0).sum(),(diab.SkinThickness==0).sum(),(diab.Insulin==0).sum(),(diab.BMI==0).sum(),(diab.DiabetesPedigreeFunction==0).sum(),(diab.Age==0).sum()
## Counting cells with 0 Values for each variable and publishing the counts below
Inference:¶
- As Zero Counts of some the variables are as high as 374 and 227, in a 768 data set, it is better to remove the Zeros uniformly for 5 variables (excl Pregnancies & Outcome)
- As a next step, we’ll drop 0 values and create a our new dataset which can be used for further analysis
## Creating a dataset called 'dia' from original dataset 'diab' with excludes all rows with have zeros only for Glucose, BP, Skinthickness, Insulin and BMI, as other columns can contain Zero values.
drop_Glu=diab.index[diab.Glucose == 0].tolist()
drop_BP=diab.index[diab.BloodPressure == 0].tolist()
drop_Skin = diab.index[diab.SkinThickness==0].tolist()
drop_Ins = diab.index[diab.Insulin==0].tolist()
drop_BMI = diab.index[diab.BMI==0].tolist()
c=drop_Glu+drop_BP+drop_Skin+drop_Ins+drop_BMI
dia=diab.drop(diab.index[c])
dia.info()
Inference¶
- As in above, created a cleaned up list titled “dia” which has 392 rows of data instead of 768 from original list
- Looks like we lost nearly 50% of data but our data set is now cleaner than before
- In fact the removed values can be used for Testing during modeling. So actually we haven’t really lost them completly.
Performing Preliminary Descriptive Stats on the Data set¶
- Performing 5 number summary
- Usually, the first thing to do in a data set is to get a hang of vital parameters of all variables and thus understand a little bit about the data set such as central tendency and dispersion
dia.describe()
Split the data frame into two sub sets for convenience of analysis¶
- As we wish to study the influence of each variable on Outcome (Diabetic or not), we can subset the data by Outcome
- dia1 Subset : All samples with 1 values of Outcome
- dia0 Subset: All samples with 0 values of Outcome
dia1 = dia[dia.Outcome==1]
dia0 = dia[dia.Outcome==0]
dia1
dia0
Graphical screening for variables¶
- Now we will start graphical analysis of outcome. At the data is nominal(binary), we will run count plot and compute %ages of samples who are diabetic and non-diabetic
## creating count plot with title using seaborn
sns.countplot(x=dia.Outcome)
plt.title("Count Plot for Outcome")
# Computing the %age of diabetic and non-diabetic in the sample
Out0=len(dia[dia.Outcome==1])
Out1=len(dia[dia.Outcome==0])
Total=Out0+Out1
PC_of_1 = Out1*100/Total
PC_of_0 = Out0*100/Total
PC_of_1, PC_of_0
Inference on screening Outcome variable¶
- There are 66.8% 1’s (diabetic) and 33.1% 0’s (nondiabetic) in the data
- As a next step, we will start screening variables
Graphical Screening for Variables¶
- We will take each variable, one at a time and screen them in the following manner
- Study the data distribution (histogram) of each variable – Central tendency, Spread, Distortion(Skewness & Kurtosis)
- To visually screen the association between ‘Outcome’ and each variable by plotting histograms & Boxplots by Outcome value
Screening Variable – Pregnancies¶
## Creating 3 subplots - 1st for histogram, 2nd for histogram segmented by Outcome and 3rd for representing same segmentation using boxplot
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.set_style("dark")
plt.title("Histogram for Pregnancies")
sns.distplot(dia.Pregnancies,kde=False)
plt.subplot(1,3,2)
sns.distplot(dia0.Pregnancies,kde=False,color="Blue", label="Preg for Outome=0")
sns.distplot(dia1.Pregnancies,kde=False,color = "Gold", label = "Preg for Outcome=1")
plt.title("Histograms for Preg by Outcome")
plt.legend()
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome,y=dia.Pregnancies)
plt.title("Boxplot for Preg by Outcome")
Inference on Pregnancies¶
- Visually, data is right skewed. For data of count of pregenancies. A large proportion of the participants are zero count on pregnancy. As the data set includes women > 21 yrs, its likely that many are unmarried
- When looking at the segemented histograms, a hypothesis is the as pregnancies includes, women are more likely to be diabetic
- In the boxplots, we find few outliers in both subsets. Esp some non-diabetic women have had many pregenancies. I wouldn’t be worried.
- To validate this hypothesis, need to statistically test.
Screening Variable – Glucose¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
plt.title("Histogram for Glucose")
sns.distplot(dia.Glucose, kde=False)
plt.subplot(1,3,2)
sns.distplot(dia0.Glucose,kde=False,color="Gold", label="Gluc for Outcome=0")
sns.distplot(dia1.Glucose, kde=False, color="Blue", label = "Gloc for Outcome=1")
plt.title("Histograms for Glucose by Outcome")
plt.legend()
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome,y=dia.Glucose)
plt.title("Boxplot for Glucose by Outcome")
Inference on Glucose¶
- 1st graph – Histogram of Glucose data is slightly skewed to right. Understandably, the data set contains over 60% who are diabetic and its likely that their Glucose levels were higher. But the grand mean of Glucose is at 122.\
- 2nd graph – Clearly diabetic group has higher glucose than non-diabetic.
- 3rd graph – In the boxplot, visually skewness seems acceptable (<2) and its also likely that confidence intervels of the means are not overlapping. So a hypothesis that Glucose is measure of outcome, is likely to be true. But needs to be statistically tested.
Screening Variable – Blood Pressure¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.distplot(dia.BloodPressure, kde=False)
plt.title("Histogram for Blood Pressure")
plt.subplot(1,3,2)
sns.distplot(dia0.BloodPressure,kde=False,color="Gold",label="BP for Outcome=0")
sns.distplot(dia1.BloodPressure,kde=False, color="Blue", label="BP for Outcome=1")
plt.legend()
plt.title("Histogram of Blood Pressure by Outcome")
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome,y=dia.BloodPressure)
plt.title("Boxplot of BP by Outcome")
Inference on Blood Pressure¶
- 1st graph – Distribution looks normal. Mean value is 69, well within normal values for diastolic of 80. One should expect this data to be normal, but as we don’t know if the particpants are only hypertensive medication, we can’t comment much.
- 2nd graph – Most non diabetic women seem to have nominal value of 69 and diabetic women seems to have high BP.
- 3rd graph – Few outliers in the data. Its likely that some people have low and some have high BP. So the association between diabetic (Outcome) and BP is an suspect and needs to be statistically validated.
Screening Variable – Skin Thickness¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.distplot(dia.SkinThickness, kde=False)
plt.title("Histogram for Skin Thickness")
plt.subplot(1,3,2)
sns.distplot(dia0.SkinThickness, kde=False, color="Gold", label="SkinThick for Outcome=0")
sns.distplot(dia1.SkinThickness, kde=False, color="Blue", label="SkinThick for Outcome=1")
plt.legend()
plt.title("Histogram for SkinThickness by Outcome")
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome, y=dia.SkinThickness)
plt.title("Boxplot of SkinThickness by Outcome")
Inferences for Skinthickness¶
- 1st graph – Skin thickness seems be be skewed a bit.
- 2nd graph – Like BP, people who are not diabetic have lower skin thickness. This is a hypothesis that has to be validated. As data of non-diabetic is skewed but diabetic samples seems to be normally distributed.
Screening Variable – Insulin¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.distplot(dia.Insulin,kde=False)
plt.title("Histogram of Insulin")
plt.subplot(1,3,2)
sns.distplot(dia0.Insulin,kde=False, color="Gold", label="Insulin for Outcome=0")
sns.distplot(dia1.Insulin,kde=False, color="Blue", label="Insuline for Outcome=1")
plt.title("Histogram for Insulin by Outcome")
plt.legend()
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome, y=dia.Insulin)
plt.title("Boxplot for Insulin by Outcome")
Inference for Insulin¶
- 2hour serum insulin is expected to be between 16 to 166. Clearly there are Outliers in the data. These Outliers are concern for us and most of them with higher insulin values ar also diabetic. So this is a suspect.
Screening Variable – BMI¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.distplot(dia.BMI, kde=False)
plt.title("Histogram for BMI")
plt.subplot(1,3,2)
sns.distplot(dia0.BMI, kde=False,color="Gold", label="BMI for Outcome=0")
sns.distplot(dia1.BMI, kde=False, color="Blue", label="BMI for Outcome=1")
plt.legend()
plt.title("Histogram for BMI by Outcome")
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome, y=dia.BMI)
plt.title("Boxplot for BMI by Outcome")
Inference for BMI¶
- 1st graph – There are few outliers. Few are obese in the dataset. Expected range is between 18 to 25. In general, people are obese
- 2nd graph – Diabetic people seems to be only higher side of BMI. Also the contribute more for outliers
- 3rd graph – Same inference as 2nd graph
Screening Variable – Diabetes Pedigree Function¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.distplot(dia.DiabetesPedigreeFunction,kde=False)
plt.title("Histogram for Diabetes Pedigree Function")
plt.subplot(1,3,2)
sns.distplot(dia0.DiabetesPedigreeFunction, kde=False, color="Gold", label="PedFunction for Outcome=0")
sns.distplot(dia1.DiabetesPedigreeFunction, kde=False, color="Blue", label="PedFunction for Outcome=1")
plt.legend()
plt.title("Histogram for DiabetesPedigreeFunction by Outcome")
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome, y=dia.DiabetesPedigreeFunction)
plt.title("Boxplot for DiabetesPedigreeFunction by Outcome")
Inference of Diabetes Pedigree Function¶
- I dont know what this variable is. But it doesn’t seem to contribute to diabetes
- Data is skewed. I don’t know if his parameter is expected to be a normal distribution. Not all natural parameters are normal
- As DPF increases, there seems to be a likelihood of being diabetic, but needs statistical validation
Screening Variable – Age¶
plt.figure(figsize=(20, 6))
plt.subplot(1,3,1)
sns.distplot(dia.Age,kde=False)
plt.title("Histogram for Age")
plt.subplot(1,3,2)
sns.distplot(dia0.Age,kde=False,color="Gold", label="Age for Outcome=0")
sns.distplot(dia1.Age,kde=False, color="Blue", label="Age for Outcome=1")
plt.legend()
plt.title("Histogram for Age by Outcome")
plt.subplot(1,3,3)
sns.boxplot(x=dia.Outcome,y=dia.Age)
plt.title("Boxplot for Age by Outcome")
Inference for Age¶
- Age is skewed. Yes, as this is life data, it is likely to fall into a weibull distribution and not normal
- There is a tendency that as people age, they are likely to become diabetic. This needs statistical validation
- But diabetes, itself doesn’t seem to have an influence of longetivity. May be it impacts quality of life which is not measured in this data set.
Normality Test¶
Inference: None of the variables are normal. (P>0.05) May be subsets are normal
## importing stats module from scipy
from scipy import stats
## retrieving p value from normality test function
PregnanciesPVAL=stats.normaltest(dia.Pregnancies).pvalue
GlucosePVAL=stats.normaltest(dia.Glucose).pvalue
BloodPressurePVAL=stats.normaltest(dia.BloodPressure).pvalue
SkinThicknessPVAL=stats.normaltest(dia.SkinThickness).pvalue
InsulinPVAL=stats.normaltest(dia.Insulin).pvalue
BMIPVAL=stats.normaltest(dia.BMI).pvalue
DiaPeFuPVAL=stats.normaltest(dia.DiabetesPedigreeFunction).pvalue
AgePVAL=stats.normaltest(dia.Age).pvalue
## Printing the values
print("Pregnancies P Value is " + str(PregnanciesPVAL))
print("Glucose P Value is " + str(GlucosePVAL))
print("BloodPressure P Value is " + str(BloodPressurePVAL))
print("Skin Thickness P Value is " + str(SkinThicknessPVAL))
print("Insulin P Value is " + str(InsulinPVAL))
print("BMI P Value is " + str(BMIPVAL))
print("Diabetes Pedigree Function P Value is " + str(DiaPeFuPVAL))
print("Age P Value is " + str(AgePVAL))
Screening of Association between Variables to study Bivariate relationship¶
- We will use pairplot to study the association between variables – from individual scatter plots
- Then we will compute pearson correlation coefficient
- Then we will summarize the same as heatmap
sns.pairplot(dia, vars=["Pregnancies", "Glucose","BloodPressure","SkinThickness","Insulin", "BMI","DiabetesPedigreeFunction", "Age"],hue="Outcome")
plt.title("Pairplot of Variables by Outcome")
Inference from Pair Plots¶
- From scatter plots, to me only BMI & SkinThickness and Pregnancies & Age seem to have positive linear relationships. Another likely suspect is Glucose and Insulin.
- There are no non-linear relationships
- Lets check it out with Pearson Correlation and plot heat maps
cor = dia.corr(method ='pearson')
cor
sns.heatmap(cor)
Inference from ‘r’ values and heat map¶
- No 2 factors have strong linear relationships
- Age & Pregnancies and BMI & SkinThickness have moderate positive linear relationship
- Glucose & Insulin technically has low correlation but 0.58 is close to 0.6 so can be assumed as moderate correlation
Final Inference before model building¶
- Data set contains many zero values and they have been removed and remaining data has been used for screening and model building
- Nearly 66% of participants are diabetic in the sample data
- Visual screening (boxplots and segmented histograms) shows that few factors seem to influence the outcome
- Moderate correlation exists between few factors and so while building model, this has to be borne in mind. If co-correlated factors are included, it might lead to Inflation of Variance.
- As a next step, a binary logistic regression model has been built
Logistic Regression¶
- A logistic regression is used from the dependent variable is binary, ordinal or nominal and the independent variables are either continuous or discrete
- In this scenario, a Logit Model has been used to fit the data
- In this case an event is defined as occurance of ‘1’ in outcome
- Basically logistic regression uses the odds ratio to build the model
cols=["Pregnancies", "Glucose","BloodPressure","SkinThickness","Insulin", "BMI","DiabetesPedigreeFunction", "Age"]
X=dia[cols]
y=dia.Outcome
## Importing stats models for running logistic regression
import statsmodels.api as sm
## Defining the model and assigning Y (Dependent) and X (Independent Variables)
logit_model=sm.Logit(y,X)
## Fitting the model and publishing the results
result=logit_model.fit()
print(result.summary())
Inference from the Logistic Regression¶
- The R sq value of the model is 56%.. that is this model can explain 56% of the variation in dependent variable
- To identify which variables influence the outcome, we will look at the p-value of each variable. We expect the p-value to be less than 0.05(alpha risk)
- When p-value<0.05, we can say the variable influences the outcome
- Hence we will eliminate Diabetes Pedigree Function, Age, Insulin and re run the model
2nd itertion of the Logistic Regression with fewer variables¶
cols2=["Pregnancies", "Glucose","BloodPressure","SkinThickness","BMI"]
X=dia[cols2]
logit_model=sm.Logit(y,X)
result=logit_model.fit()
print(result.summary2())
Inference from 2nd Iteration¶
- We will now eliminate BMI and re run the model
3rd iteration of Logistic Regression¶
cols3=["Pregnancies", "Glucose","BloodPressure","SkinThickness"]
X=dia[cols3]
logit_model=sm.Logit(y,X)
result=logit_model.fit()
print(result.summary())
Inference from 3rd Iteration¶
- Now the P value of skinthickness is greater than 0.05, hence we will eliminate it and re run the model
4th Iteration of Logistic Regression¶
cols4=["Pregnancies", "Glucose","BloodPressure"]
X=dia[cols4]
logit_model=sm.Logit(y,X)
result=logit_model.fit()
print(result.summary())
Inference from 4th Run¶
- Now the model is clear. We have 3 variables that influence the Outcome and then are Pregnancies, Glucose and BloodPressure
- Luckly, none of these 3 variables are co-correlated. Hence we can safetly assume tha the model is not inflated
## Importing LogisticRegression from Sk.Learn linear model as stats model function cannot give us classification report and confusion matrix
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
cols4=["Pregnancies", "Glucose","BloodPressure"]
X=dia[cols4]
y=dia.Outcome
logreg.fit(X,y)
## Defining the y_pred variable for the predicting values. I have taken 392 dia dataset. We can also take a test dataset
y_pred=logreg.predict(X)
## Calculating the precision of the model
from sklearn.metrics import classification_report
print(classification_report(y,y_pred))
Precision of the model is 77%¶
from sklearn.metrics import confusion_matrix
## Confusion matrix gives the number of cases where the model is able to accurately predict the outcomes.. both 1 and 0 and how many cases it gives false positive and false negatives
confusion_matrix = confusion_matrix(y, y_pred)
print(confusion_matrix)
The result is telling us that we have 234+69 are correct predictions and 61+28 are incorrect predictions.¶
Is TQM relevant in the age of Artificial Intelligence & Industry 4.0?
Digital Transformation, Artificial Intelligence, Industry 4.0, IoT, RPA, etc are some of the buzz words that are bringing shivers in the spine of many executives. To be fair, actually many are excited about the future and the opportunities that these tools and methods present.
One side of the coin
A few months ago, in a conversation with the Head of Business Excellence of a MNC in manufacturing sector where TQM & other similar practices are deeply rooted, he said that this year their focus is Industry 4.0 and there are no budgets for any other initiative. He said that TQM, Lean Six Sigma, etc are concepts that are gone past their half life and in this new age, everything will be automated sooner or later. So no Kaizens will be needed, no Six Sigma DMIAC projects will be needed and so is Value Stream Mapping. And as automated processes are highly efficient, there will be no need for improvement projects. He had a point. Instead of dismissing the idea or accepting, it is good to consider how to navigate through these new age developments.
Now the other side of the coin
Another friend of mine who steers strategy and business development for a global digital transformation solutions provideracross sectors recently reached out to me. The quest was to find ways to help their clients to speed up the adoption of digital technologies and reduce internal resistance. He said the problem was to do with their culture. Here is a quick summary of what transpired:
- Internal acceptance and adoption is slow for digital transformation technologies and expected ROI remains an aspiration
- Digital Transformation is a journey and not a ‘fix it and forget it’ model. In reality, it is a continuum of iterative improvements leading to big transformation
- A successful Digital Transformation should devote 80% effort in people behavior change and only 20% in technology change
- To sustain Digital gains, every employee should wear the hat of improvement specialist such as a Six Sigma Black Belt.
- If every competitor of yours uses the same technology, you would have no definitive advantage. Ultimately what to differentiate and how to differentiate will come from your employees and technology will only be an enabler
- There is no substitute to employee engagement and involvement
So, there is no doubt that new Digital technologies will put you in a new orbit, but soon that orbit will become a slow lane. In the ’90s, ERP wave swept the industry, then it was CRM, and then BI, and then Cloud, and then Big Data, and now it is AI, Robotics & IoT.
So ultimately these technology tools enable business but nothing can beat an organization that has the following competencies ingrained in their culture:
- Leaders are grounded and their priorities are clear
- Everyone has a quest to challenge status quo and improve the way they work
- Employees treat and participate like one does in a family
- Business models are built around Customers and not Technology
- Decisions are factual & inclusive
Whether you call it Agile, DevOps, Six Sigma, Lean, TQM or BE, these frameworks rely on the same fundamental principles mentioned above.
So, to sum up TQM or any such Business Excellence frameworks are enablers for Digital Transformation and cannot be replaced by AI, IoT, Industry 4.0
After few months, when we talked again, he said they are strategizing on Industry 4.0 and not started any real work.
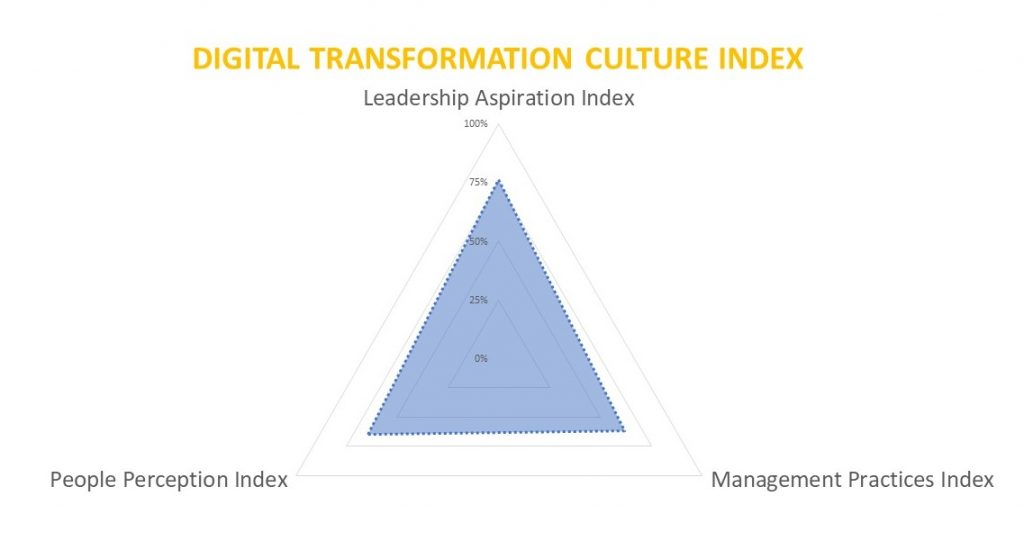
We have created an assessment to evaluate the Digital Transformation Culture of an organization. There are 3 broad areas –
- Leadership Aspiration Index – What leaders are aspiring vs reality
- Management Practices Index – What management practices are needed vs reality
- People Perception Index – What people think vs reality
Gap assessment will be in the following manner:
Sign-up for collaborat newsletter